ГИА и ЕГЭ по информатике: Системы счисления

Тема: Системы счисления

Система счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.

Система счисления:

даёт представления множества чисел (целых и/или вещественных);
даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление);
отражает алгебраическую и арифметическую структуру чисел.

Системы счисления подразделяются на позиционные, непозиционные и смешанные.

Наиболее употребляемыми в настоящее время позиционными системами являются:

2 — двоичная (в дискретной математике, информатике, программировании);
3 — троичная;
8 — восьмеричная;
10 — десятичная (используется повсеместно);
12 — двенадцатеричная (счёт дюжинами);
13 — тринадцатеричная;
16 — шестнадцатеричная (используется в программировании, информатике);
60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).

В позиционных системах чем больше основание системы, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.

Двоичная запись чисел В двоичной системе счисления числа записываются с помощью двух символов (0 и 1). Чтобы не путать в какой системе счисления записано число его снабжают указателем справа внизу. Таким образом, положительное целое число (без знака) x в двоичной системе счисления записывается в виде:

$x = (a_{n-1} a_{n-2}\dots a_{1} a_0)_2 = \sum_{k=0}^{n-1} a_k 2^k$ ,

где:

$x$ — представляемое число,
$a_k$ — цифры из множества {0,1},
$n$ — количество цифр (знаков) в числе x,
$k$ — порядковый номер цифры.

Целые числа со знаком записываются в виде:

$x = (z a_{n-1} a_{n-2}\dots a_{1} a_0)_2 = z \sum_{k=0}^{n-1} a_k 2^k$ ,

где:

$z$ — знак числа из множества {+,-}, у положительных целых чисел знак зачастую опускается.

Дробные числа записываются в виде:

$x = (a_{n-1} a_{n-2} \dots a_{1} a_{0}, a_{-1} a_{-2} \dots a_{-(m-1)} a_{-m})_2 = \sum_{k=-m}^{n-1} a_k 2^k$ ,

где:

$m$ — число цифр дробной части числа,
$a_k$ — цифры из множества $\{0,1\}$ .

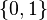В двоичной системе счисления (как и в других системах счисления, кроме десятичной) знаки читаются по одному. Например, число 101₂ произносится «один ноль один».

(Материал из Википедии)

1) Некоторое число в двоичной системе счисления записывается как 1100001. Определите число и запишите его в ответе в десятичной системе счисления.

Ответ: для перевода двоичных чисел в десятичные воспользуемся методом Горнера: надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). 1100001

0*2+1=1.

1*2+1=3.

3*2+0=6

6*2+0=12

12*2+0=24

24*2+0=48

48*2+1=97

{Первым числом всегда должен быть 0. Умножаем его на основу системы (2) и прибавляем первое двоичное число. Затем ответ умножаем на 2 и прибавляем второе двоичное число и т.д.}

ГИА и ЕГЭ по информатике

Популярные сообщения

Системы счисления

Комментариев нет:

Отправить комментарий

Архив блога

Обо мне